Clasificación de ecuaciones lineales o de primer grado |
Sabemos que una ecuación lineal o de primer grado es aquella que involucra solamente sumas y restas de variables elevadas a la primera potencia (elevadas a uno, que no se escribe). Son llamadas lineales por que se pueden representar como rectas en el sistema cartesiano.
Se pueden presentar tres tipos de ecuaciones lineales:
a) ecuaciones lineales propiamente tales
En este tipo de ecuación el denominador de todas las expresiones algebraicas es igual a 1 (no se presentan como fracción, aunque el resultado sí puede serlo).
Para proceder a la resolución se debe:
Eliminar paréntesis.
Dejar todos los términos que contengan a "x" en un miembro y los números en el otro.
Luego despejar "x" reduciendo términos semejantes.
Ejemplo:
Ejemplo:
4x – 2(6x – 5) = 3x + 12(2x + 16)
4x – 12x + 10 = 3x + 24x + 192
4x – 12x – 3x – 24x = 192 – 10
–35x = 182
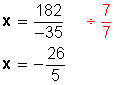
b) ecuaciones fraccionarias
En este tipo de ecuación lineal el denominador de a lo menos una de las expresiones algebraicas es diferente de 1 (es una fracción).
Para proceder a la resolución se debe:
Llevar a ecuación lineal (eliminar la fracción) multiplicando la ecuación por el mínimo común múltiplo de los denominadores (m.c.m.)
Ejemplo:
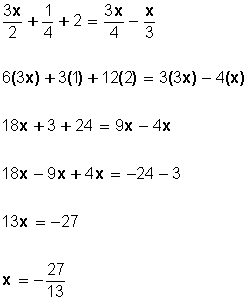
m.c.m. de 2, 4 y 3 = 12
c) ecuaciones literales
Pueden ser lineales o fraccionarias. Si son fraccionarias, se llevan al tipo lineal, pero en el paso de reducir términos semejantes se factoriza por "x" para despejarla.
Ejemplo:
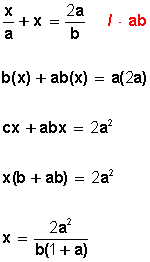
Sistema de ecuaciones lineales
https://www.youtube.com/watch?v=LDJCl59hX7c
En matemáticas y álgebra lineal, un sistema de ecuaciones lineales, también conocido como sistema lineal de ecuaciones o simplemente sistema lineal, es un conjunto de ecuaciones lineales (es decir, un sistema de ecuaciones en donde cada ecuación es de primer grado), definidas sobre un cuerpo o un anillo conmutativo. Un ejemplo de sistema lineal de ecuaciones sería el siguiente:
El problema consiste en encontrar los valores desconocidos de las variables x1, x2 y x3 que satisfacen las tres ecuaciones.
El problema de los sistemas lineales de ecuaciones es uno de los más antiguos de la matemática y tiene una infinidad de aplicaciones, como en procesamiento digital de señales, análisis estructural, estimación, predicción y más generalmente en programación lineal así como en la aproximación de problemas no lineales de análisis numérico.
Introducción[editar]
En general, un sistema con m ecuaciones lineales y n incógnitas puede ser escrito en forma normal como:
Donde  son las incógnitas y los números
son las incógnitas y los números 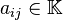 son los coeficientes del sistema sobre el cuerpo
son los coeficientes del sistema sobre el cuerpo ![\mathbb{K}\ [= \R, \mathbb{C}, \dots]](http://upload.wikimedia.org/math/d/d/1/dd172d7f353ca18a891dda59a0d44cc5.png) . Es posible reescribir el sistema separando con coeficientes con notación matricial:
. Es posible reescribir el sistema separando con coeficientes con notación matricial:
 son las incógnitas y los números
son las incógnitas y los números 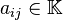 son los coeficientes del sistema sobre el cuerpo
son los coeficientes del sistema sobre el cuerpo ![\mathbb{K}\ [= \R, \mathbb{C}, \dots]](http://upload.wikimedia.org/math/d/d/1/dd172d7f353ca18a891dda59a0d44cc5.png) . Es posible reescribir el sistema separando con coeficientes con notación matricial:
. Es posible reescribir el sistema separando con coeficientes con notación matricial:(1)
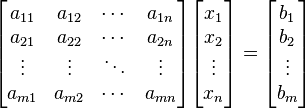
Si representamos cada matriz con una única letra obtenemos:
Donde A es una matriz m por n, x es un vector columna de longitud n y b es otro vector columna de longitud m. El sistema de eliminación de Gauss-Jordan se aplica a este tipo de sistemas, sea cual sea el cuerpo del que provengan los coeficientes. La matriz A se llama matriz de coeficientes de este sistema lineal. A b se le llama vector de términos independientes del sistema y a x se le llama vector de incógnitas.
Una ecuación es una igualdad donde por lo menos hay un número desconocido, llamado incógnita o variable, y que se cumple para determinado valor numérico de dicha incógnita.
Se denominan ecuaciones lineales o de primer grado a las igualdades algebraicas con incógnitas cuyo exponente es 1 (elevadas a uno, que no se escribe).
Como procedimiento general para resolver ecuaciones enteras de primer grado se deben seguir los siguientes pasos:
1. Se reducen los términos semejantes, cuando es posible.
2. Se hace la transposición de términos (aplicando inverso aditivo o multiplicativo), los que contengan la incógnita se ubican en el miembro izquierdo, y los que carezcan de ella en el derecho.
3. Se reducen términos semejantes, hasta donde es posible.
4. Se despeja la incógnita, dividiendo ambos miembros de la ecuación por el coeficiente de la incógnita (inverso multiplicativo), y se simplifica.
Resolución de ecuaciones de primer grado con una incógnita
Para resolver ecuaciones de primer grado con una incógnita, aplicamos el criterio del operador inverso (inverso aditivo o inverso multiplicativo), como veremos en el siguiente ejemplo:
Resolver la ecuación 2x – 3 = 53
Debemos tener las letras a un lado y los números al otro lado de la igualdad (=), entonces para llevar el –3 al otro lado de la igualdad, le aplicamos el inverso aditivo (el inverso aditivo de –3 es +3, porque la operación inversa de la resta es la suma).
Entonces hacemos:
2x – 3 + 3 = 53 + 3
En el primer miembro –3 se elimina con +3 y tendremos:
2x = 53 + 3
2x = 56
Ahora tenemos el número 2 que está multiplicando a la variable o incógnita x, entonces lo pasaremos al otro lado de la igualdad dividiendo. Para hacerlo, aplicamos el inverso multiplicativo de 2 (que es ½) a ambos lados de la ecuación:
2x • ½ = 56 • ½
Simplificamos y tendremos ahora:
x = 56 / 2
x = 28
Entonces el valor de la incógnita o variable "x" es 28.
Ver: PSU: Matemática,
Ver: Resolución de ecuaciones
Resolvamos otros ejemplos:
Llevamos los términos semejantes a un lado de la igualdad y los términos independientes al otro lado de la igualdad (hemos aplicado operaciones inversas donde era necesario).
| |
Resolvemos las operaciones indicadas anteriormente.
| |
Aplicamos operaciones inversas, y simplificamos.
|
(pasamos todos los términos con “x” a la izquierda, cambiado el signo 8x pasa como – 8x)
| |
(redujimos los términos semejantes en el primer miembro: 5x – 8x = – 3x)
| |
(dividimos ambos términos por – 3 para despejar la “x”)
| |
(– 15 dividido – 3 es igual a 5. Número negativo dividido por un número negativo, el resultado es positivo)
|
(pasamos a la derecha los términos conocidos, en este caso sólo +1 que pasa como – 1)
| |
(reducción de términos semejantes: 2 – 1 = 1)
| |
(dividimos ambos términos por 4 para que, al simplificar 4/4 quede la x sola).Esto es lo mismo que tener 4x = 1 y simplemente pasar a la derecha como divisor el 4 que en la izquierda está multiplicando.
| |
(léase, menos un tercio). La fracción es negativa pues se divide un positivo, el 1, con un negativo, el – 3.
|
Resolución de ecuaciones con agrupaciones de signos
Para resolver este tipo de ecuaciones primero debemos suprimir los signos de agrupación considerando la ley de signos, y en caso de existir varias agrupaciones, desarrollamos de adentro hacia afuera las operaciones.
Veamos el siguiente ejemplo:
Primero quitamos los paréntesis.
| |
Reducimos términos semejantes.
| |
Ahora quitamos los corchetes.
| |
Transponemos los términos, empleando el criterio de operaciones inversas.
| |
Nuevamente reducimos términos semejantes
| |
Despejamos x pasando a dividir a – 2, luego simplificamos.
|
Advertencia
Para suprimir los signos de agrupación debemos tener en cuenta que:
a) Si tenemos un signo + antes de un signo de agrupación no afecta en nada a lo que esté dentro de este signo. Por ejemplo: +(3x – 5) = 3x – 5
b) Si por el contrario, tenemos un signo – antes del signo de agrupación, este signo afectará a todo lo que esté dentro del signo.Todos los términos dentro del signo de agrupación cambiarán de signo. Por ejemplo: –(3x – 5) = – 3x + 5
Resolución de ecuaciones con productos incluidos
Para resolver este tipo de ecuaciones, primero se efectúan los productos incluidos y luego se sigue el procedimiento general (aplicando el criterio de las operaciones inversas).
Observemos un ejemplo:
Resolvemos el producto indicado, y adicionalmente eliminamos los paréntesis.
| |
Llevamos los términos semejantes a un lado de la igualdad, y los términos independientes al otro lado (empleamos operaciones inversas.)
| |
Reducimos términos semejantes en ambos lados de la igualdad.
| |
Despejamos x pasando 3 a dividir.
|
Resolución de problemas mediante ecuaciones
Para resolver un problema, debemos plantearlo en forma matemática y luego realizar las operaciones correspondientes para hallar el valor de la incógnita (el dato que deseamos conocer).
Veamos un problema característico:
Pedro es 3 años menor que Álvaro, pero es 7 años mayor que María. Si la suma de las edades de los tres es 38, ¿qué edad tiene cada uno?
Digamos que las edades de los tres son:
x edad de Pedro
y edad de Álvaro
z edad de María
y edad de Álvaro
z edad de María
Sabemos que la edad de Álvaro es igual a la edad de Pedro más 3 años (Pedro es tres años menor que Álvaro):
y = x + 3
También sabemos que la edad de María es igual a la edad de Pedro menos 7 años (Pedro es 7 años mayor que María):
z = x – 7
Ahora tenemos que:
edad de Pedro: x
edad de Álvaro: x +3
edad de María: x – 7
La suma de las tres edades es 38:
x + x +3 + x – 7 = 38
Resolviendo está última ecuación tendremos:
x = 14 (esta es la edad de Pedro)
Finalmente:
edad de Pedro: x = 14 años
edad de Álvaro: x + 3 = 17 años
edad de María: x – 7 = 7 años
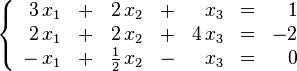
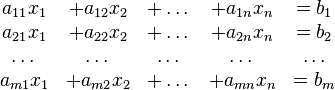
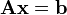
No hay comentarios:
Publicar un comentario