Física
Cinemática
< Física
La cinemática es una rama de la física dedicada al estudio del movimiento de los cuerpos en el espacio, sin atender a las causas que lo producen (lo que llamamos fuerzas). Por tanto la cinemática sólo estudia el movimiento en sí, a diferencia de la dinámica que estudia las interacciones que lo producen. El Análisis Vectorial es la herramienta matemática más adecuada para ellos.
En cinemática distinguimos las siguientes partes:
La magnitud vectorial de la Cinematica fundamental es el "desplazamiento" Δs, que experimenta un cuerpo durante un lapso Δt. Como el desplazamiento es un vector, por consiguiente, sigue la ley del paralelogramo, o la ley de suma vectorial. Asi si un cuerpo realiza un desplazamiento "consecutivo" o "al mismo tiempo" dos desplazamientos 'a' y 'b', nos da un deslazamiento igual a la suma vectorial de 'a'+'b' como un solo desplazamiento.

Dos movimientos al mismo tiempo entran principalmente, cuando un cuerpo se mueve respecto a un sistema de referencia y ese sistema de referencia se mueve relativamente a otro sistema de referencia. Ejemplo: El movimiento de un viajero en un tren en movimiento, que esta siendo visto por un observador desde el terraplén. O cuando uno viaja en coche y observa las montañas y los arboles a su alrededor.
Observación sobre la notación: en el texto y en la ilustración se nombra a los vectores con letras negrillas y cursivas. En las fórmulas y ecuaciones, que se escriben con TeX, son vectores los que tienen una flecha sobre sus letras
Contenido
[ocultar]Conceptos....[editar]
Modelo físico: Para estudiar la realidad, los físicos se sirven de 'modelos' que, con cierta aproximación y en determinadas condiciones, corresponden con ella. Se usan para realizar cálculos teóricos. Así, puede modelizarse un balón con una esfera para, por ejemplo, calcular su volumen con cierta aproximación conociendo su radio aproximado, aunque no es exactos.
Punto: Es un modelo físico. Se refiere a un elemento de volumen despreciable (se considerará sin volumen) situado en el espacio (en 3D. Busca 'espacio euclidiano' para más detalles).
Posición: Llamamos posición de un punto a su localización con respecto a un sistema de referencia (lo que en física se llama 'observador').
Sistema de referencia: Es aquel sistema coordenado con respecto al cual se da la posición de los puntos y el tiempo (a determinadas velocidades el tiempo cambia, buscad la paradoja de los gemelos). Profundizaremos más en este tema cuando se aborde el de Movimiento relativo.
Tiempo: Por nuestro lenguaje parece complicado de definir. Los griegos dieron una solución que, por ahora, nos puede valer. Llamamos tiempo al contínuo transcurrido entre dos instantes.
Partícula puntual: Es un modelo físico. Se refiere a un elemento de tamaño diferencial (muy pequeño) y masa concentrada en su posición.
Sólido rígido o, simplemente, sólido: Es otro modelo físico. Puede definirse de varias formas. La más usada es la que lo hace como un cuerpo cuyas distancias entre partículas permanecen constantes con el tiempo. Aunque ésto no ocurre en la realidad, para esfuerzos moderados una mesa seguira siendo rígida, pero un globo puede no responder a éste modelo.
Rapidez y aceleración[editar]
Diariamente escuchamos los conceptos de rapidez y aceleración como velocidad y aceleración solamente. Pero en física la velocidad y la aceleración son vectores, por lo que es claro y necesario su diferenciación y entendimiento. De aquí en adelante (más por costumbre que por ganas) llamaremos tanto a la rapidez y a la aceleración solamente como velocidad y aceleración (a menos que se especifique lo contrario).
Si cubre una masa puntual en un punto P en un tiempo Δt el tramo Δs, se llamara al cociente Δs / Δt su velocidad media vm en el intervalo de tiempo Δt o en el tramo Δs.
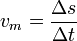
Se observa que Δs aquí no es el desplazamiento, sino la longitud de arco: es el camino recorrido.
La llamamos velocidad media porque la masa puntual no se mueve por el trayecto uniforme trazado. O sea estamos tomando sólo los puntos final e inicial para hacer los cálculos.
Hagamos el trayecto como Δs (de manera diferencial, o sea infinitesimal), al igual que al intervalo de tiempo Δt. Para Δs cercano a cero (o Δt cercano a cero, que tienda a cero) el cociente Δs/Δt como valor al límite, nos da la velocidad v de la masa puntual en el punto P, así:
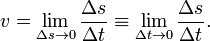
En el análisis se puede calcular ese valor al límite también como ds/dt. Así:

Tomemos luego una masa puntual que tiene en el punto P y en el tiempo t la velocidad v; y en el tiempo t + Δt y la velocidad v + Δv. Podemos calcular el cociente Δv/Δt como la aceleración media am de la masa puntual en el intervalo de tiempo Δt:
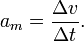
Para Δt cercano a cero se aspira a que ese cociente tenga un valor límite, la aceleracion a de la masa puntual para el tiempo t.
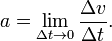
Para ese valor límite, se puede simplificar:
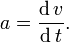
Es el camino s descrito como una función analítica del tiempo t, así s=s(t), así es la función de velocidad v(t) la primera derivada de la función s(t) con respecto al tiempo, la función de aceleración a(t) es la segunda derivada. La derivación con respecto al tiempo se puede también escribir como un punto sobre las variables.

En sentido contrario se puede encontrar la función de velocidad y la función de la trayectoria a través de la integración:

En las integrales indefinidas de debe aumentar una constante que puede ser conocida con las condiciones iniciales del problema.
Ejemplo: En caida libre una masa puntual se encuentra con una aceleración constante g. Esto es, cuando el tiempo t=0 verticalmente de arriba hacia abajo, tiene la velocidad v0 y sus coordenadas s0:
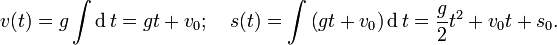
Velocidad y aceleración vectorial[editar]
Velocidad[editar]
Vamos a ver ahora a una partícula, que atraviesa un espacio en una curva. Para el tiempo t se halla en P, para el tiempo t + Δt en Q. El lugar del punto esta descrito por su vector posición 'r'. Esta es una función de t y esta descrita por una función vectorial 'r'(t).
Asi:

y

donde i, j y k son los vectores unitarios de los ejes de cordenadas.
El desplazamiento de la partícula en un determinado intervalo de tiempo es:

El cociente Δr/Δt es la velocidad media (vectorial) vm de la partícula en el intervalo de tiempo Δt. Es

Aqui es (mirar arriba: rapidez y aceleración) Δx/Δt la rapidez media de la partícula paralela al eje X, Δy/Δt la rapidez media paralela al eje Y y Δz/Δt la rapidez media paralela al eje Z en un intervalo Δt.
El vector resultante, del cociente Δr/Δt para Δt cercano a cero, se llama velocidad vP = v'(t) de la particula en P o en el tiempo t.
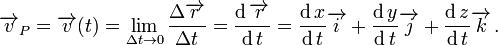
La función vectorial v'(t) es la primera derivada de la función de posición r(t) en el tiempo.

Como se ve, son las componentes escalares del vector v(t) identicos con la velocidad instantanea paralela a los ejes:

El recta en el punto P en la direccion del vector vP se llama La Tangente a la curva en P
Aceleración[editar]
Análogamente vamos ahora a definir la función vectorial de la aceleración:

La función vectorial de la aceleración proviene de las componentes escalares de la función velocidad y de la función posición, así:
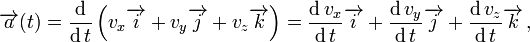
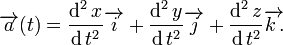
Como se conoce, son las componentes escalares del vector velocidad igual a la dirección de la velocidad instantánea en los ejes de coordenadas.
En sentido contrario se puede hallar por integración las correspondientes funciones.
Ejemplo: Para la caída libre con velocidad inicial v0 de un punto con el vector posición r0 (vertical o lanzamiento curvo).
Cuando el eje Z (vector unitario k) esta dirigido verticalmente hacia abajo, es
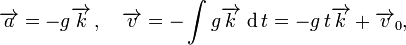

Mientras el vector velocidad siempre tiene dirección tangencial, puede estar dirigido opcionalmente el vector aceleración. En un análisis profundo, la aceleración se descompone en dos componentes, en la una dirección es tangencial (aceleración tangencial) y la otra esta en dirección vertical (aceleración normal).
La aceleración tangencial cambia solo el valor de la velocidad (esta es la rapidez)
Para esta descomposición de los vectores de la aceleración introducimos la curva s, este es el largo de la trayectoria, que recorre la partícula en la curva. Este arco cuenta con un punto cero escogido, que de todas formas aquí no juega ningún papel, aquí solo necesitamos el diferencial ds del arco. Además introducimos el vector unitario tangencial t y hacemos uso de la geometría diferencial. El vector unitario tangente t es el vector
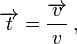
así denominado, es igual al vector v dividido para su módulo v. Este módulo es igual a la rapidez y es otra vez el desplazamiento sobre la curva sobre el tiempo. Asi es:
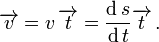
Si diferenciamos para el tiempo tenemos que

Aqui la longitud del vector unitario tangencial t es constante (cercano a 1), esta el vector desplazamiento dt/ds - cuando no es igual a cero - verticalmente hacia t.
De la geometría diferencial tenemos, que el vector desplazamiento dt/ds
- tiene la dirección del vector unitario normal n y
- el valor k = 1/ρ
De aquí es k la curvatura de la curva en el punto observado y ρ su radio de curvatura. El vector unitario normal n es dirigido hacia (momentaneamente) un punto medio de la curvatura (hacia dentro).
Siguiendo esto
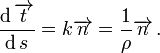
Con esto nos da como resultado
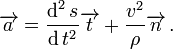
El vector a esta entre t y n' dirigido, en el plano de la curva en un determinado punto.
El modulo de la aceleración tangencial es - como se esperaba:
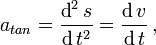
el modulo de la aceleración normal es
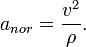
Este par de ecuaciones tienen su interpretación: La aceleración de una partícula da lugar a la aparición de una fuerza. La dirección de esa fuerza determina la dirección de la aceleración. La componente tangencial de la aceleración causa un cambio en la velocidad, la componente normal de la aceleración causa la curvatura de la curva. El radio de curvatura de la curva en un determinado punto resulta de la aceleración normal y de la velocidad así:
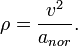
Movimiento circular[editar]
Una particula P se mueve en una circunferencia. Colocamos un eje de coordenadas XY y en el origen O del sistema de coordenadas en el centro de la circunferencia.
Entonces es
Analogo a la velocidad y a la aceleracion podemos definir la velocidad angular ω así
y a la aceleracion angular α
Cuando t = 0 es también φ = 0, entonces es
Movimiento circular uniforme[editar]
Un movimiento circular con velocidad angular constante se lo llama uniforme. Entonces
La ecuacion del vector posición es
Con esto nos da la velocidad
y
Efectuando el producto escalar entre los vectores r y v obtenemos:
Con lo cual resulta que los vectores r y v son perpendiculares. Para la aceleracion tenemos que
y así
La aceleracion esta dirigida hacia O (aceleracion centripeta), y su modulo es constante.
Movimiento circular uniformemente acelerado[editar]
Aqui la aceleracion angular α es constante y también ω(0) = 0
También, cuando φ(0)=0, así para el angulo de rotacion
Asi tenemos también que
y
o
Asi, podemos dedecir que la componente radial de la aceleracion (y su direccion) es
y su componente tangencial es
La velocidad angular como medida de direccion[editar]
A veces es muy util ver a la velocidad angular como medida de la direccion y representarlo a traves de un en el eje de giro y su modulo sea igual a la velocidad angular. Asi se introduce un vector unitario a la medida ω e como el vector vector. O sea su falta lo esencial e indispensable propiedad de los vmysytrymrtectores: esta no puede sudos movimientos de rotacion (donde ambas partes de la velocidad deban ser investigadas particularmente) es util la introducción de unos vectores de rotacion.
Ecuaciones de Movimiento en un sistema de coordenadas polares[editar]
Velocidad en coordenadas Polares[editar]
La velocidad v de una partícula material puede descomponerse en distintos tipos de componentes. Es usual e importante que se descomponga en componentes que tengan la dirección de los ejes de coordenadas, así se obtiene en la forma siguiente:
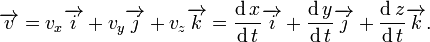
Otra alternativa puede ahora ser representado en un eje XY


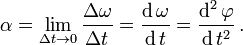
![\varphi \left( t \right) = \int_0^t {\omega \,\operatorname{d} t} = \int_0^t {\left[ {\int_0^t {\alpha \,\operatorname{d} t} } \right]} \operatorname{d} t\,.](http://upload.wikimedia.org/math/2/7/5/2757758ecbebc67cf48d72a125ae8851.png)
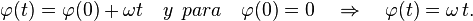
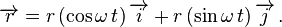


![\begin{align}
\overrightarrow r \, \cdot \overrightarrow v & = r\left( {\cos \omega \,t} \right) \left[- r\omega \left( {\sin \omega \,t} \right)\right] + r\left( {\sin \omega \,t} \right) r\omega \left( {\cos \omega \,t} \right) \\
& = - r^2 \omega \left( {\sin \omega \,t} \right)\left( {\cos \omega \,t} \right) + r^2 \omega \left( {\sin \omega \,t} \right)\left( {\cos \omega \,t} \right) \\
& = 0
\end{align}](http://upload.wikimedia.org/math/e/f/f/eff82b88dacb6d147a1289bf9db14f1d.png)


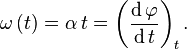
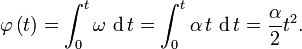

![\overrightarrow v = \frac{{\operatorname{d} \overrightarrow r }}
{{\operatorname{d} t}} = r\alpha \,t\left[ { - \left( {\sin \,\frac{\alpha }
{2}t^2 } \right)\overrightarrow i + \left( {\cos \frac{\alpha }
{2}t^2 } \right)\overrightarrow j } \right] = r\omega \left[ { - \left( {\sin \,\frac{\alpha }
{2}t^2 } \right)\overrightarrow i + \left( {\cos \frac{\alpha }
{2}t^2 } \right)\overrightarrow j } \right]](http://upload.wikimedia.org/math/5/2/6/526163d5925d1e0013eec1449ba3d8af.png)
![\overrightarrow a = \frac{{\operatorname{d} \overrightarrow v }}
{{\operatorname{d} t}} = r\alpha \left[ { - \left( {\sin \frac{\alpha }
{2}t^2 } \right)\overrightarrow i + \left( {\cos \frac{\alpha }
{2}t^2 } \right)\overrightarrow j } \right] +](http://upload.wikimedia.org/math/f/2/b/f2b7abd36b7ab46a91072ea3380cba89.png)
![+ \,r\alpha ^2 t^2 \left[ {\left( { - \cos \frac{\alpha }
{2}t^2 } \right)\overrightarrow i - \left( {\sin \frac{\alpha }
{2}t^2 } \right)\overrightarrow j } \right].](http://upload.wikimedia.org/math/6/f/2/6f22ae3c30a183200b9931ef6f9853dc.png)
![\overrightarrow a = \left[ { - r\alpha \left( {\sin \varphi } \right) - r\omega ^2 \left( {\cos \varphi } \right)} \right]\overrightarrow i +](http://upload.wikimedia.org/math/9/1/2/91211942147a28de3d28e927d9ec6122.png)
![+ \left[ {r\alpha \left( {\cos \varphi } \right) - r\omega ^2 \left( {\sin \varphi } \right)} \right]\overrightarrow j .](http://upload.wikimedia.org/math/7/1/3/71347ae6734f4b755258039108b9ca70.png)


No hay comentarios:
Publicar un comentario